Note
Click here to download the full example code
Time-evolving parameter estimation¶
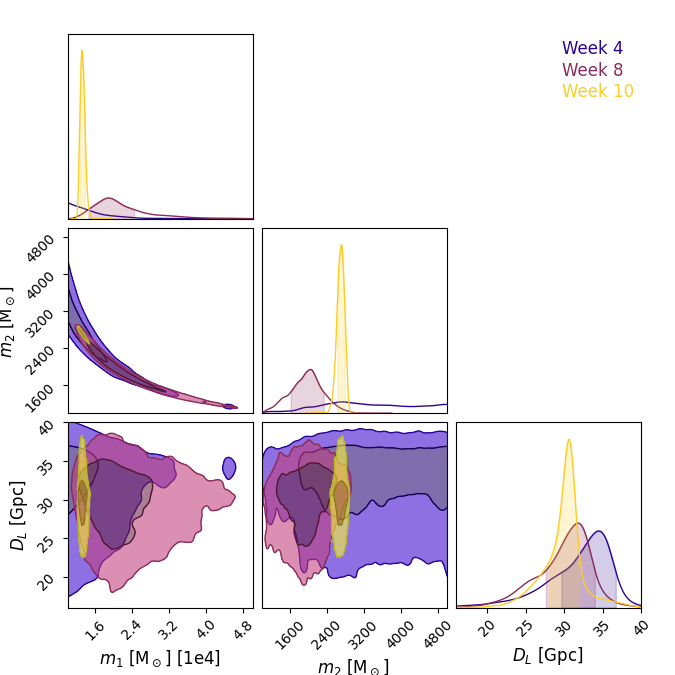
Corner plot of select parameters for a single source showing how parameter estimation changes with observing time.
import matplotlib.pyplot as plt
from chainconsumer import ChainConsumer
from lisacattools.catalog import GWCatalogs
from lisacattools.catalog import GWCatalogType
# Find the list of catalogs
catPath = "../../tutorial/data/mbh"
catalogs = GWCatalogs.create(GWCatalogType.MBH, catPath, "*.h5")
last_cat = catalogs.get_last_catalog()
detections_attr = last_cat.get_attr_detections()
detections = last_cat.get_detections(detections_attr)
Choose a source from the list of detections and get its history through the different catalogs Pick a source, any source
sourceIdx = "MBH005546845"
Load chains for different observing epochs of selected source Get source history and display table with parameters and observing weeks containing source
srcHist = catalogs.get_lineage(last_cat.name, sourceIdx)
srcHist.drop_duplicates(subset="Log Likelihood", keep="last", inplace=True)
srcHist.sort_values(by="Observation Week", ascending=True, inplace=True)
srcHist[
[
"Observation Week",
"Parent",
"Log Likelihood",
"Mass 1",
"Mass 2",
"Luminosity Distance",
]
]
# Load chains for different observing epochs of selected source
allEpochs = catalogs.get_lineage_data(srcHist)
Create corner for multiple observing epochs
# Choose weeks for plot from source history table
wks = [4, 8, 10]
# select subset of parameters to plot
parameters = ["Mass 1", "Mass 2", "Luminosity Distance"]
parameter_labels = [
r"$m_1\ [{\rm M}_\odot]$",
r"$m_2\ [{\rm M}_\odot]$",
r"$D_L\ [{\rm Gpc}]$",
]
ranges = [(10000, 50000), (1000, 5000), (16, 40)]
c = ChainConsumer()
for idx, wk in enumerate(wks):
epoch = allEpochs[allEpochs["Observation Week"] == wk]
samples = epoch[parameters].values
c.add_chain(samples, parameters=parameter_labels, name="Week " + str(wk))
c.configure(cmap="plasma")
fig = c.plotter.plot(figsize=1.5, log_scales=False, extents=ranges)
plt.show()
Total running time of the script: ( 0 minutes 3.145 seconds)