Note
Click here to download the full example code
Corner plots¶
Produce corner plots for a single sources’ parameters.
Load catalog and select individual source
import matplotlib.pyplot as plt
import numpy as np
from lisacattools.catalog import GWCatalog
from lisacattools.catalog import GWCatalogs
from lisacattools.catalog import GWCatalogType
# load catalog
catPath = "../../tutorial/data/ucb"
catalogs = GWCatalogs.create(GWCatalogType.UCB, catPath, "cat15728640_v2.h5")
final_catalog = catalogs.get_last_catalog()
detections_attr = final_catalog.get_attr_detections()
detections = final_catalog.get_detections(detections_attr)
# get index of source with maximum SNR
sourceId = detections.index.values[
np.argmin(np.abs(np.array(detections["SNR"]) - detections["SNR"].max()))
]
detections.loc[[sourceId], ["SNR", "Frequency"]]
Corner plot of select source parameters using corner module
import corner
# read in the chain samples for this source
samples = final_catalog.get_source_samples(sourceId)
# list of subset of paramters that are particularly interesting
parameters = ["Frequency", "Frequency Derivative", "Amplitude", "Inclination"]
# corner plot of source.
fig = corner.corner(samples[parameters])
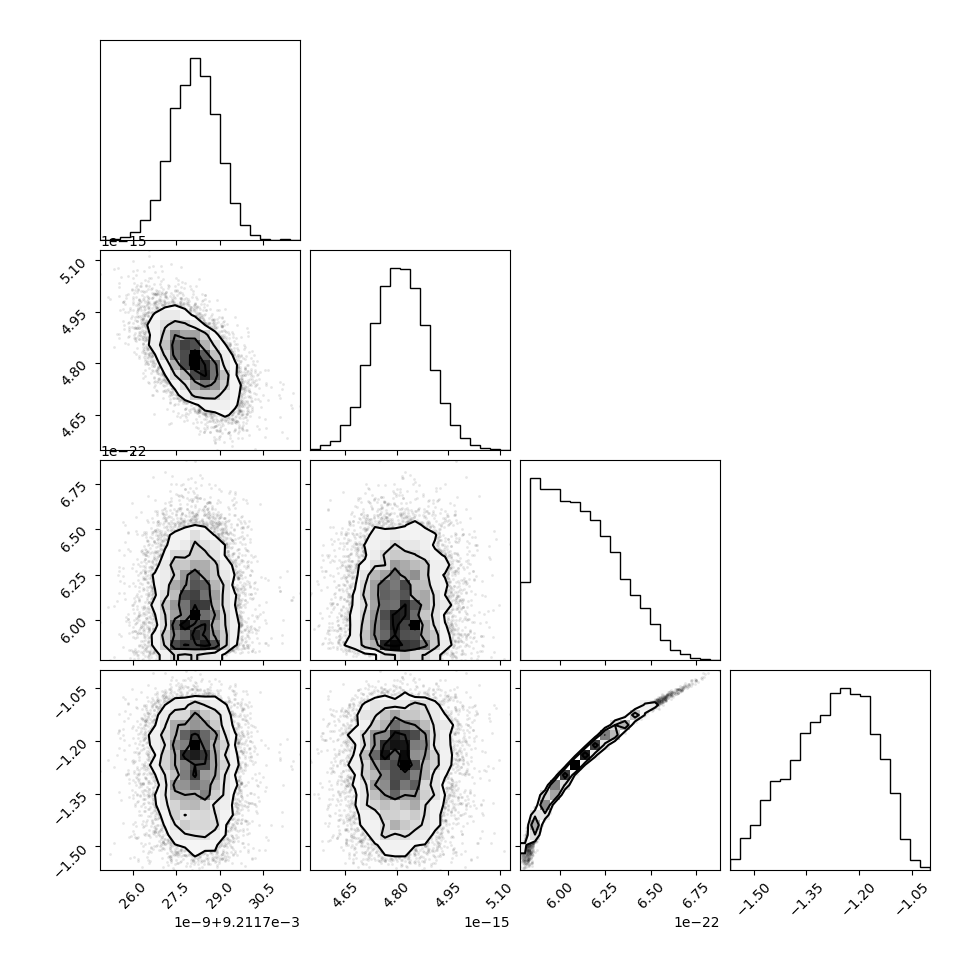
Can also be done with ChainConsumer for prettier plots
from chainconsumer import ChainConsumer
# get dataframe into numpy array (this shouldn't be necessary)
df = samples[parameters].values
# rescale columns
df[:, 0] = df[:, 0] * 1000 # f in mHz
df[:, 1] = df[:, 1] / 1e-15 # df/dt
df[:, 2] = df[:, 2] / 1e-22 # A
df[:, 3] = df[:, 3] * 180.0 / np.pi # inc in deg
parameter_symbols = [
r"$f\ {\rm [mHz]}$",
r"$\dot{f}\ [s^{-2}]\times 10^{-16}$",
r"$\mathcal{A} \times 10^{-23}$",
r"$\iota\ {\rm [deg]}$",
]
# add source chain to ChainConsumer object
c = ChainConsumer().add_chain(df, parameters=parameter_symbols, cloud=True)
# plot!
fig = c.plotter.plot(figsize=1.5)
plt.show()
![$f\ {\rm [mHz]} = \left( 92117281.7^{+7.6}_{-8.4} \right) \times 10^{-7}$, $\dot{f}\ [s^{-2}]\times 10^{-16} = 4.817^{+0.070}_{-0.088}$, $\mathcal{A} \times 10^{-23} = 5.864^{+0.372}_{-0.040}$, $\iota\ {\rm [deg]} = -70.6^{+5.7}_{-8.3}$](../_images/sphx_glr_plot_source_parameters_002.png)
Total running time of the script: ( 0 minutes 2.186 seconds)